launchctl: Bootstrap failed: 5: Input/output error
2025-09-26
Initial symtoms
We have an internal service that needs to start a boot. The responsible team wrote a simple launchd script, like this:
<?xml version="1.0" encoding="UTF-8"?>
<!DOCTYPE plist PUBLIC "-//Apple//DTD PLIST 1.0//EN" "http://www.apple.com/DTDs/PropertyList-1.0.dtd">
<plist version="1.0">
<dict>
<key>Label</key>
<string>com.example.watchdog</string>
<key>ProgramArguments</key>
<array>
<string>/usr/local/bin/watchdog</string>
</array>
<key>RunAtLoad</key>
<true/>
<key>KeepAlive</key>
<true/>
<key>SessionCreate</key>
<true/>
<key>StandardOutPath</key>
<string>/var/log/watchdog.out</string>
<key>StandardErrorPath</key>
<string>/var/log/watchdog.err</string>
</dict>
</plist>
Helix returns "No definition found" when going to a definition
2025-08-14
If you follow this blog regularly, you know that I’m so happy with the combo WezTerm (terminal emulator) and Helix (editor). Since I recently switched to a project that uses Java, I’m trying to configure Helix as my Java editor.
The default language server for Java is jdtls which can be installed easily on macOS by running:
brew install jdtls
hx --health java
Configured language servers:
✓ jdtls: /opt/homebrew/bin/jdtls
Configured debug adapter: None
Configured formatter: None
Tree-sitter parser: ✓
Highlight queries: ✓
Textobject queries: ✓
Indent queries: ✓
Tags queries: ✓
Rainbow queries: ✓
What I'm doing now
2025-03-28
After taking some time to refresh myself and going on a road trip through Vietnam, I returned to the office to work as a Platform Engineer for a company in Hanoi. I’m learning to write an OS in Rust while continuing to read OSTEP. I’m building an all-in-one troubleshooting tool named diagtree, where I turn nearly any command into a tree, helping me quickly debug multiple services across different environments, from local to testing, and production.
Uses
2024-02-27
I found uses.tech and would like to add myself.
Hardware
- MacBook Pro (14-inch, 2021)
- Magic Keyboard
- Magic Mouse
- Nexstand K2 (to save my neck): https://www.youtube.com/watch?v=-fzlZAecI_4
- Raspberry Pi 4: host this website
Development
- Terminal: WezTerm
- Shell: fish shell
- Text Editor: Helix
Tools
- Git: lazygit, tig
- HTTP client: xh
- ls: exa
- cat: bat
- find: fd
- Search: ag
- Quick jump: zoxide
- Fuzzy finder: fzf
- Watch for changes: entr
- GitHub CLI: gh
- Container runtimes: colima
Integration testing TUI applications in Rust
2024-01-21
In building games with any language, there will be a loop to handle the key events. In case of crossterm, it’s event::read:
if poll(Duration::from_millis(10))? {
let event = read()?;
match event {
Event::Key(KeyEvent {
code,
state: _,
kind,
modifiers: _,
}) => {
if kind == KeyEventKind::Press {
let mut tetromino = self.current_tetromino.clone();
match code {
KeyCode::Char('h') | KeyCode::Left => {
tetromino.move_left(self, stdout)?;
self.current_tetromino = tetromino;
}
libp2p performance benchmarking
2023-10-27
I invested some time in studying QUIC and libp2p In this article, I will show you how to benchmark the network transfer using perf module for 2 scanerios:
- high latency, no packet loss
- low latency but high packet loss
Let’s print help first:
Running `rust-libp2p/target/debug/perf -h`
Usage: perf [OPTIONS]
Options:
--server-address <SERVER_ADDRESS>
--transport <TRANSPORT>
--upload-bytes <UPLOAD_BYTES>
--download-bytes <DOWNLOAD_BYTES>
--run-server Run in server mode
-h, --help Print help
Learning Rust by building Tetris: my favorite childhood game
2023-10-03

After completing the Rust book and working through rustlings, I found myself standing at the crossroads, wondering where to go next. It was then that I had an idea - a project that would allow me to apply my newfound knowledge and create something meaningful. My favorite childhood game, Tetris, became the inspiration for my next coding adventure.
Since I want it to be playable on Windows, I chose the TUI library crossterm.
Turning Helix into an IDE with the help of WezTerm and CLI tools
2023-08-19

This post recaps previous series of posts about Helix.
- Running code
- Jumping to build errors
- Quickly select a command and open it in a new pane
- Testing a single function
- Git integration
- File tree
- Creating snippets
- How to debug?
- Interactive global search
- Opening file in GitHub
1. Running code
In my previous post, I shared a method for running code from within Helix by using this PR.
I later discovered another useful trick here. We can use wezterm cli get-text command to extract the filename and line number from the status line:
Debug Rust in Helix using lldb-vscode: display the contents of local string variables
2023-08-11
In a previous post titled debugging Rust in Helix,
I introduced a workaround using codelldb to address the visualization issue related to string variables within lldb-vscode.
However, the usage of codelldb presents some challenges:
- We have to start the server first using
codelldb --port 13000 - It is noticeably slow
- The Helix theme breaks when listing variables
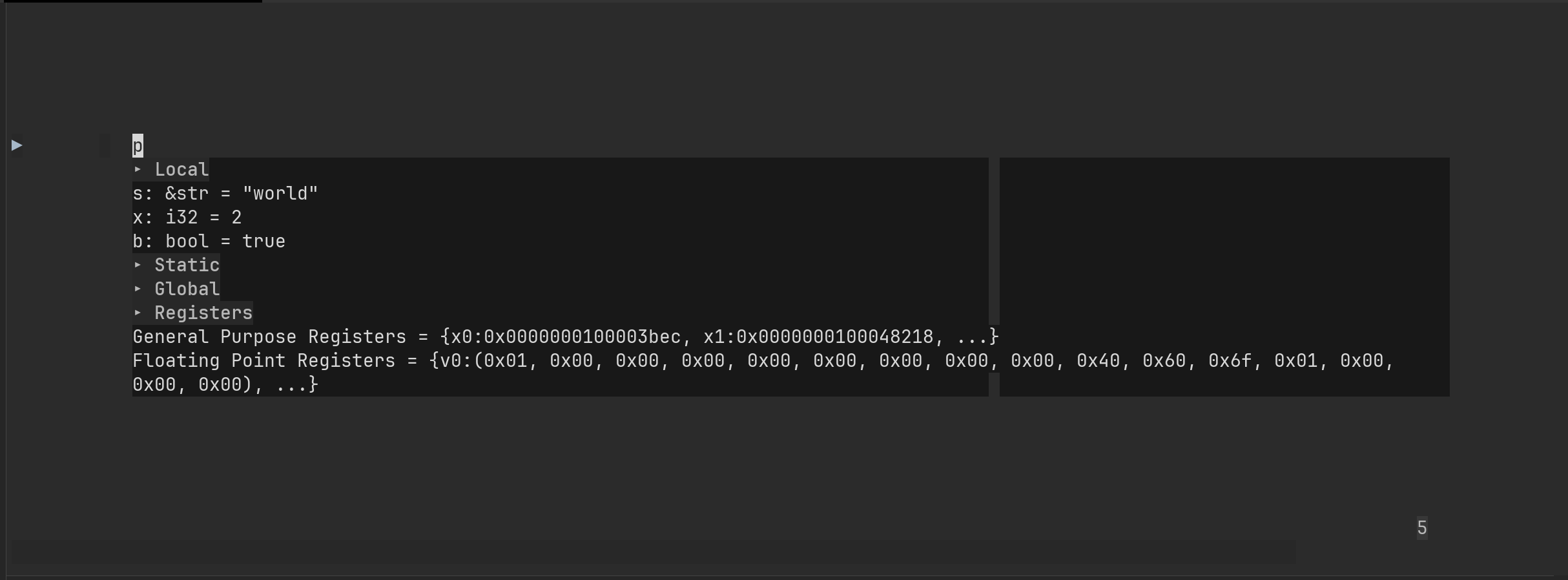
In my quest for an improved debugging experience, I found rust-lldb, which impressively manages to display the contents of string variables:
How to debug Rust in Helix?
2023-08-10
Helix supports debugging Rust by default using lldb-vscode. However, there is an issue where string variables are displayed as memory addresses instead of their actual values:
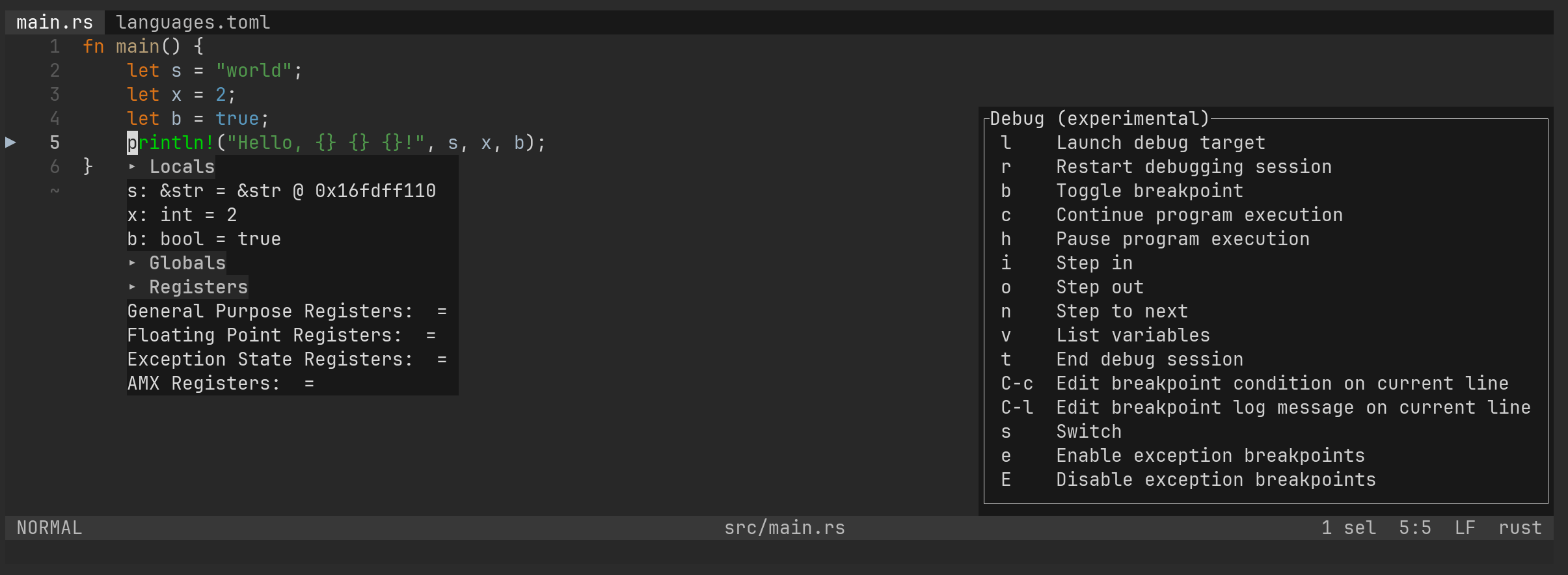
Noticing that CodeLLDB natively supports visualization of most common Rust data types, I would like to give it a try.
Here’s the step-by-step process:
Download the CodeLLDB extension:
$ cd ~/Downloads/
$ wget https://github.com/vadimcn/codelldb/releases/download/v1.9.2/codelldb-aarch64-darwin.vsix
Setup the extension:
$ mkdir -p ~/.local
$ set fish_user_paths /Users/quantong/.local/extension/adapter $fish_user_paths
$ codelldb
If you encountered this error:
 Quan Tong
Quan Tong