Quan Tong
"Life is all about sharing. If we are good at something, pass it on." - Mary Berry

What I'm doing now

2025-03-28

After taking some time to refresh myself and going on a road trip through Vietnam, I returned to the office to work as a Platform Engineer for a company in Hanoi. I’m learning to write an OS in Rust while continuing to read OSTEP. I’m building an all-in-one troubleshooting tool named diagtree, where I turn nearly any command into a tree, helping me quickly debug multiple services across different environments, from local to testing, and production.

Read More...

Uses

2024-02-27

I found uses.tech and would like to add myself.

Hardware

Development

Tools

Read More...

Integration testing TUI applications in Rust

2024-01-21

In building games with any language, there will be a loop to handle the key events. In case of crossterm, it’s event::read:

 1if poll(Duration::from_millis(10))? {
 2    let event = read()?;
 3    match event {
 4        Event::Key(KeyEvent {
 5            code,
 6            state: _,
 7            kind,
 8            modifiers: _,
 9        }) => {
10            if kind == KeyEventKind::Press {
11                let mut tetromino = self.current_tetromino.clone();
12                match code {
13                    KeyCode::Char('h') | KeyCode::Left => {
14                        tetromino.move_left(self, stdout)?;
15                        self.current_tetromino = tetromino;
16                    }

Read More...

libp2p performance benchmarking

2023-10-27

I invested some time in studying QUIC and libp2p In this article, I will show you how to benchmark the network transfer using perf module for 2 scanerios:

Let’s print help first:

 1     Running `rust-libp2p/target/debug/perf -h`
 2Usage: perf [OPTIONS]
 3
 4Options:
 5      --server-address <SERVER_ADDRESS>
 6      --transport <TRANSPORT>
 7      --upload-bytes <UPLOAD_BYTES>
 8      --download-bytes <DOWNLOAD_BYTES>
 9      --run-server                       Run in server mode
10  -h, --help                             Print help

Read More...

Learning Rust by building Tetris: my favorite childhood game

2023-10-03

Play tetris 2-player mode in the terminal

After completing the Rust book and working through rustlings, I found myself standing at the crossroads, wondering where to go next. It was then that I had an idea - a project that would allow me to apply my newfound knowledge and create something meaningful. My favorite childhood game, Tetris, became the inspiration for my next coding adventure.

Since I want it to be playable on Windows, I chose the TUI library crossterm.

Read More...

Turning Helix into an IDE with the help of WezTerm and CLI tools

2023-08-19

Helix as IDE

This post recaps previous series of posts about Helix.

  1. Running code
  2. Jumping to build errors
  3. Quickly select a command and open it in a new pane
  4. Testing a single function
  5. Git integration
  6. File tree
  7. Creating snippets
  8. How to debug?
  9. Interactive global search
  10. Opening file in GitHub

1. Running code

In my previous post, I shared a method for running code from within Helix by using this PR.

I later discovered another useful trick here. We can use wezterm cli get-text command to extract the filename and line number from the status line:

Read More...

Debug Rust in Helix using lldb-vscode: display the contents of local string variables

2023-08-11

In a previous post titled debugging Rust in Helix, I introduced a workaround using codelldb to address the visualization issue related to string variables within lldb-vscode.

However, the usage of codelldb presents some challenges:

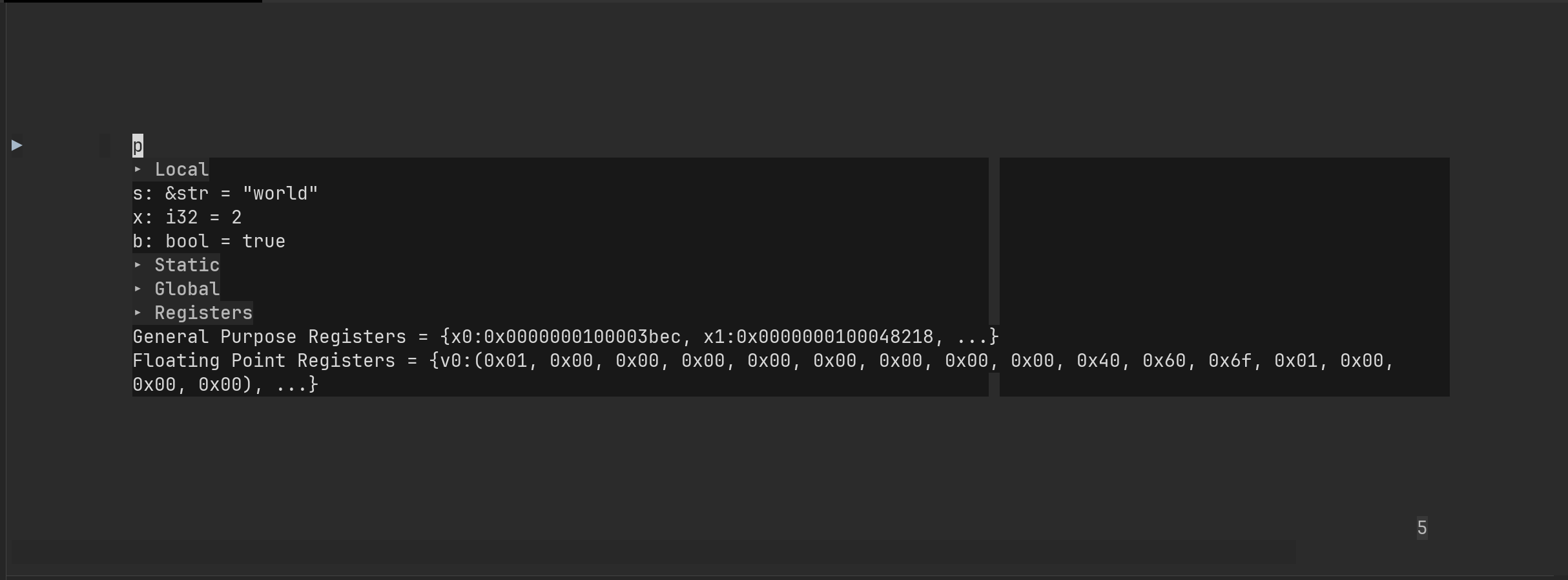
codelldb breaks helix theme

In my quest for an improved debugging experience, I found rust-lldb, which impressively manages to display the contents of string variables:

Read More...

How to debug Rust in Helix?

2023-08-10

Helix supports debugging Rust by default using lldb-vscode. However, there is an issue where string variables are displayed as memory addresses instead of their actual values:

lldb-vscode - string variables memory addresses

Noticing that CodeLLDB natively supports visualization of most common Rust data types, I would like to give it a try.

Here’s the step-by-step process:

Download the CodeLLDB extension:

1$ cd ~/Downloads/
2$ wget https://github.com/vadimcn/codelldb/releases/download/v1.9.2/codelldb-aarch64-darwin.vsix

Setup the extension:

1$ mkdir -p ~/.local
2$ set fish_user_paths /Users/quantong/.local/extension/adapter $fish_user_paths
3$ codelldb

If you encountered this error:

Read More...

nnn: wcswidth returns different values for same Unicode code point between macOS and Linux

2023-08-09

When attempting to integrate nnn with Helix, I encountered an interesting issue that resulted in duplicate first characters in the filename:

nnn duplicate first character in the filename on macOS

What’s interesting is that this issue doesn’t occur on Linux:

nnn on Linux

I’ve spent several days troubleshooting this problem but haven’t been able to identify the root cause. The only solution I could come up with is a workaround, and I must admit, I’m still not entirely satisfied with it.

Read More...

WezTerm: quickly select a command and open it in a new pane

2023-08-04

In my previous post, jump to build errors with WezTerm, I demostrated how to navigate to build error using hyperlinks. One limitation of that approach is that it requires a mouse click.

In this post, I explore how to achieve the same functionality using a shortcut key in WezTerm, thanks to QuickSelectArgs feature.

WezTerm’s QuickSelectArgs allows us to bind a shortcut key to select specific patterns and perform actions on the selected text. Let’s say we have the following warning:

Read More...